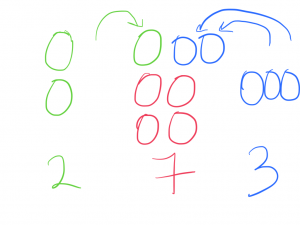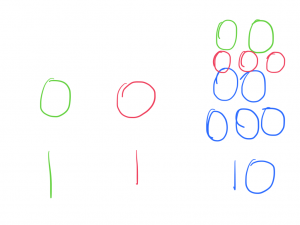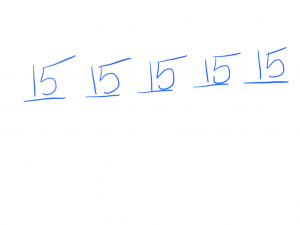Math – Solving Averages Using Rock Piles

My favorite way to solve averages problems is using Phillip Keller’s concept of rock piles from his terrific book The New Math SAT Game Plan: The Strategic Way to Score Higher. (You can download the first three chapters here.)

Back to the stone age

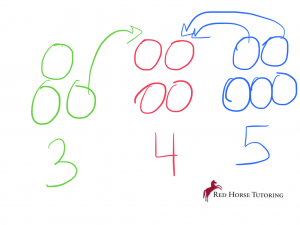
Let’s say I have 3 piles of rocks.

 

 

 

 

 

 

To find the average number of rocks in each pile, we add up all the rocks 3+4+5 = 12, divide by 3, and then get 4 as the average.

Moving rocks around

Lets see what happens when we move some rocks to a different pile.

 

 

 

 

 

 

 

 

 

 

 

 

 

What does that do to the average?  2+7+3 = 12/3 = 4. Hmm.. the average stays the same.

Piling on

What would happen if we moved all but one of the rocks in each pile to the last pile?

 

 

 

 

 

 

 

Is the average still the same? 1+1+10 = 12/3 = 4. Yep – still 4.

Aha – so you can move rocks to different piles without changing the average number of rocks in the whole pile (as long as you don’t throw away any rocks or add any new rocks to the party.)

A real SAT question

How does this work with a real SAT question?

Here is question 16 from Test 9, Section 2 on page 891 in the Blue Book. This is a medium problem.

Each of 5 people had a blank card on which they wrote a positive integer. If the average of these integers is 15, what is the greatest possible integer that could be one on of the cards?

The easiest way to start this problem it to assume that each person wrote down 15. (Phil calls this choosing the laziest numbers – making all the numbers the same as the average.)

 

 

 

 

 

 

 

If I am looking for the greatest possible integer someone could write down (the largest rock pile), then I need to minimize the number of rocks in the other piles and move the maximum number of rocks to one pile.

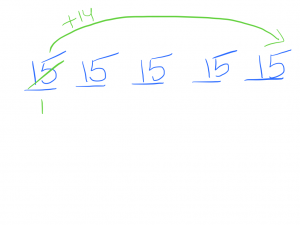
Now, let’s start moving rocks. I find it easiest to dump everything in the last pile.

So I take 14 from the first pile and dump it onto the last pile.

 

 

 

 

 

 

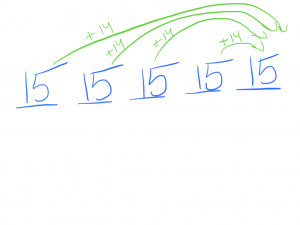
Then I do the same for the other piles.

 

 

 

 

 

 

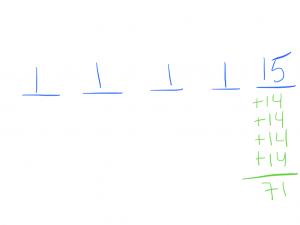
Now, I just total up the number of rocks in the last pile and that will be the greatest possible integer that one could write down and still have the average be 15.

 

 

 

 

 

 

 

Your turn

Try this one from Keller’s book for practice. Leave your answer in the comments.

A baseball team averages 5 runs scored per game over a span of 6 games. The team scored one run in the first game, two runs in the second game, three runs in the third game and four runs in the fourth game. What is the average of the runs they scored in games 5 and 6?

 

 

Image credit: E>mar at Flickr