How to Solve for Funky Shapes

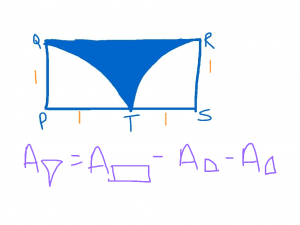
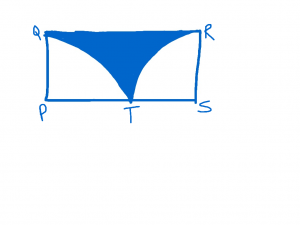
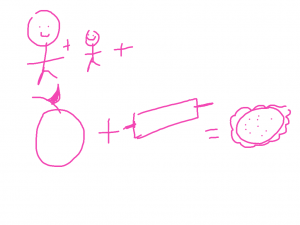In rectangle PQRS above, arc QT and RT are quarter circles with centers at P and S, respectively. If the radius of each quarter circle is 1, what is the area of the shaded region? (This a problem from the Blue Book, Test 6, Section 2, Question 16 on page 703.)

These problems drive my students crazy.

The trick is to write out a rebus or a map that shows you what you need to do.

Making apple pie

 

My little girl can’t read yet so I have to get creative when I put notes in her lunchbox.

Here I’m trying to tell her we will make an apple pie after school.

I will cut up the apples and she will roll out the dough with a rolling pin (a favorite activity) and we will put them together to make apple pie.

 

 

 

 

 

Draw your own rebus

You can use this exactly same strategy to solve funky shape problems.

 

Area of shaded area = Area of rectangle – Area of left shape – Area of right shape

 

 

 

 

 

Fill in the blanks

Now that we know what we need to do, let’s fill in the spots with numbers.

Area of rectangle

First, transfer all the info from the text to the picture. Since we know that each radius is one, the length of the rectangle is 2 and the width is 1. So the area is 2 x 1 = 2.

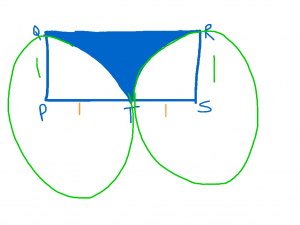
Area of the quarter-circle

It might help to draw the circles so we can clearly see that we are dealing with quarter circles.

The formula for the area of a circle is pi * r^2. Therefore a quarter circle must be 1/4 of that. So 1/4 * pi *1^2 = 1/4 pi.

 

 

 

 

 

 

 

Putting it all together

So, subbing back into our formula:

Area of funky shape = 2 –  1/4 pi – 1/4 pi.

Which simplifies to 2 – 2(1/4) pi or 2 – pi/2.

Recap

• Transfer all information in the text to the picture
• Draw out your “equation” or rebus
• Solve for each thing you need to figure out
• Put it back into the larger equation
• Solve the whole equation