Answer the question they ACTUALLY asked
(not the one you THOUGHT they asked)
I was working with a student this week on the ACT. He missed this question, not because he doesn’t know how to solve it, but because of a “silly” error.
Unforced errors are a huge problem. My kids lose more points from “silly” errors that all other error types combined (including not knowing how to solve a problem).
When I asked him how he was going to fix the problem he said that he would “try harder” and “read the question more carefully.” But in the heat of the test, good intentions go out the window.
Here’s a better tactic that prevents the majority of silly errors from happening in the first place.
The video explanation
You can watch the video or read the blog post.
Lots of triangles
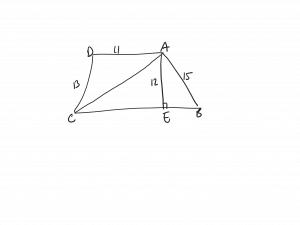 The question asked what is the area of triangle ABC?
The question asked what is the area of triangle ABC?
C. was rushing because he wanted to answer all the questions, so he assumed it was the first triangle he saw – triangle ADC.
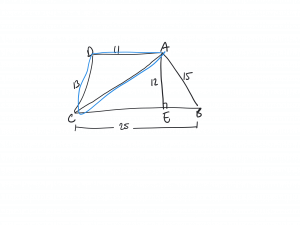
Mark up the picture, part 1
But they were asking about triangle ABC. An easy trick to just to mark up the picture with what the question is asking for. If he would have done so he would have gotten the point.
OUTLINE the triangle they are asking about. (After all, there are three different triangles they could have asked about)
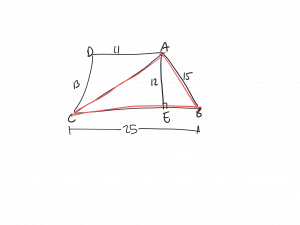
What’s your sign?
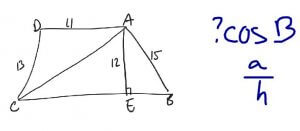
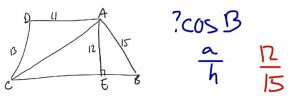
Mark up the picture, part 2
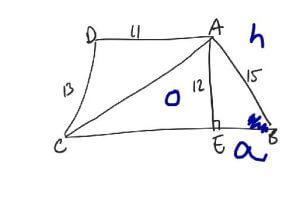
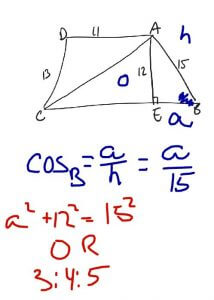
Then he could write out the formula SOHCAHTOA to remind himself of the trig formulas. From here it’s easy to see that cosine B is a/15.
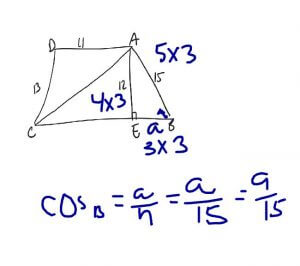
Now he needs to solve for side a. He could use the Pythagorean theorem. OR he could look at the triangle and recognize that it is a 3:4:5 triangle.
Want weekly test tips and strategies?
Subscribe to get my latest content by email.

