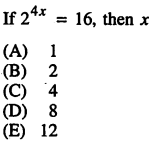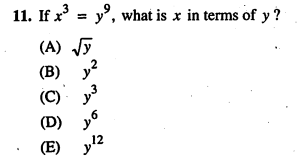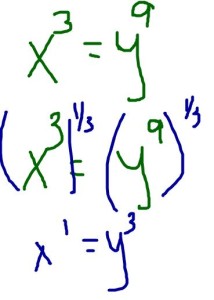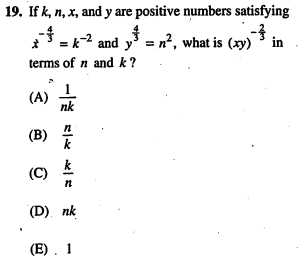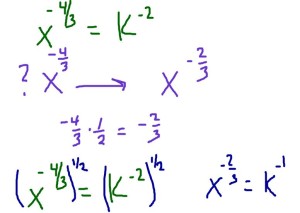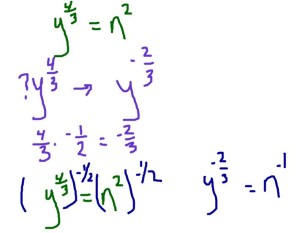Exponent problems show up frequently on the SAT. Here’s the run down on what you absolutely need to know about them in order to answer any exponent problem on the SAT.
Exponent problems show up frequently on the SAT. Here’s the run down on what you absolutely need to know about them in order to answer any exponent problem on the SAT.
You’ll need to memorize these exponent rules. (They are not listed in the handy list of formulas at the beginning of each section.)
Two caveats before we start:
It’s all about that base
The exponent rules DO NOT apply to this: 23 * 54
The exponent rules DO apply to this: 23 * 24
The magic exponent rules only apply when you have the same base!
It’s not at all about adding or subtracting those bases
You must either be multiplying, dividing or raising to a power in order to work with these exponent rules.
The exponent rules DO NOT apply to this: 23 + 24
The exponent rules DO apply to this: 23 * 24
Here are the three exponent rules that you absolutely MUST know:
1. When you multiple the same bases, you ADD the exponents
23 * 24 = 27
2. When you divide the same bases, you SUBTRACT the exponents.
23 / 24 = 2-1
3. When you raise a power to a power, you MULTIPLY the exponents.
(24)3 = 212
Let’s see this in the context of SAT exponent questions.
This is an easy question, 4.3.2, from the Official SAT Study Guide. [Note: this posts uses examples from the old SAT test. But exponents are still tested in all their glory on the new SAT test.]
I know that you can look at this problem and just figure it out.
Hmm.. 2 raised to some power is the same as 16. Hmm..2 x 2=4, 2 x 2 x 2 = 8, 2 x 2 x 2 x 2 = 16. Ah…2 raised to the 4th is 16. Therefore x must be 1.
I actually want you to think of it a different way. (A way that will make the medium and hard questions much easier to solve!)
Remember how everything needs to be in the SAME BASE.
So rewrite each side of this problem into base 2. So rewrite 16 as 24
So then you have: 24x = 24.
So since the equations are equal, then the exponents must be equal: 4x=4
x=1
If you get in the habit of automatically rewriting everything into the same base, it makes problems like 5.8.7 on page 669 much easier to solve.
Medium:
This is a tough medium question, 7.7.11, from the same book.
So we need to get to x1
Hmm.. Is there anything we can do to x3 to turn it into x1? (Hint: think MULTIPLYING)
What do I need to multiply 3 by to turn it into one? (Hint: think FRACTIONS)
Hmm..3 x 1/3 = 1. When do I multiply exponents? When I raise a power to a power.
Aha! So if I raise each side of the equation to the 1/3 power, that would solve it.
This is as hard as they get on the SAT. This is question 7.7.19 from the Blue Book. It *looks* a lot more complicated that the others, but it’s not.
Let’s start at the end. What do we want to end up with? (xy)-2/3 This can also be written as x-2/3 * y-2/3
Hmm.. how can I turn x-4/3 into x-2/3 (Hint: think multiplying by a fraction)
Let’s do the same thing for the y.
Re-read the question b/c by now I’ve forgotten what I’m supposed to be looking for.
Right. x-2/3 * y-2/3. Substituting in we get k-1 * n-1
Remember that you can rewrite a negative power like this: k-1=1/k and n-1=1/n
So (xy)-2/3 is the same as 1/k * 1/n or 1/nk
Want weekly test tips and strategies?
Subscribe to get my latest content by email.